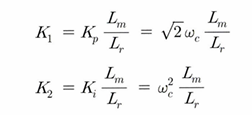우선 지난 시간에 궁금한 내용을 해결했다.
처음에 이해가 되지 않은 부분을 다시 언급하자면
유도전동기는
1. 초기에 회전 좌표계 상의 고정자 전류 지령을 갖고 있다.
2. 이를 회전각을 이용해 3상으로 역변환 후 전류제어기에 넣는다.
3. 전류제어기가 실제 전류와 오차를 계산하여 전압 지령 생성
4. 인버터가 지령만큼의 전압을 생성하여 유도 전동기에 인가
다음과 같은 과정을 걸치게 된다.
이때 처음에 우리가 주어진 값은 "회전 좌표계"상의 전류값이라 회전각을 알아야만 하는데
회전각을 구하기 위해서는
"고정 좌표계"상의 정보가 필요한 것이다.
아래에 서술할 내용에 답이 들어있었다.
1. Intro
우선 직접 벡터 제어를 하기 위해서는 자속 정보를 이용해야 한다.
이때 가장 필요한 정보는 자속 각(Theta_e)이다.

하지만 여기서는 고정좌표계 상의 회전자 쇄교자속 d,q축 성분을 요구로 한다.
아래에서는 고정자 전압을 이용한 방법(전압 모델)과 회전자 전압을 이용한 방법(전류 모델)이 등장할 것이다.
2. 고정자 전압 방정식을 이용한 자속 추정(전압 모델)
고정 좌표계의 d,q 축 회전자 쇄교 자속은 아래의 식을 이용하여 구할 수 있다.

이때 우리는 통상적으로 회전자에 흐르는 전류 정보는 알 수 없다.
따라서 회전자 전류를 다른 변수들을 이용하여 표현해야 한다.
여기서는 고정자의 d,q축 인덕턴스 식을 변형하였다.

위 식을 보면 회전자 전류가 우리가 측정할 수 있는 고정자 전류와 이미 알고있는 인덕턴스 값으로 표현된 것을 알 수있다.
이 정리된 값을 다시 회전자 쇄교 자속 식에 대입하면 아래와 같이 정리된다.

이때 아래의 누설계수를 이용해서 식을 다시 정리하였다.
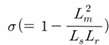
그렇다면 회전자 쇄교 자속을 구하기 위해서는 고정자 쇄교 자속과 고정자 전류가 필요한 것을 알 수 있다.
이때 고정자 전류는 그냥 말그대로 현재 유도 전동기 고정자에 흐르고 있는 전류 값이다. 따라서 우리가 흘려주고 있는 값 또는 홀센서를 이용해 측정한 값을 이용하면 된다.
그리고 고정자 쇄교 자속은 고정자 전압 방정식을 이용해서 아래와 같이 구할 수 있다.

이것을 생각하면서 위의 의문점이 해결되었다.
지금까지 나는 처음 구동을 시작하자마자 전동기가 지령치를 출력해야 한다고 생각했다.
하지만 실험을 할 때도 그렇고 실제로는 그렇지 못하다고 한다.
초기에는 그냥 랜덤하게 아무 전류나 흘러주고 그때의 고정자 전류, 전압을 측정하여
위 과정을 통해 회전 각을 만들고 그 각으로 지령을 변환해서 전류제어기에 넣어가면서 점점 오차를 줄여가는 과정인 것이다.
그래서 굳이 처음부터 지령과 일치하는 정지좌표계 변수들을 이용해서 회전각을 만들 필요가 없었던 것이다.
3. 회전자 전압 방정식을 이용한 자속 추정 (전류 모델)
위에선 고정자 전압 방정식을 이용한 것이였으면 이번에는 회전자 전압 방식을 이용해서 구해보려 한다.
우선 유도 전동기의 회전자가 농형이라면 회전자 양단의 전압은 0이라고 볼 수 있다.
이를 고려한 회전자의 전압 방정식은 아래와 같다.

이때 마찬가지로 회전자 전류 성분은 측정이 불가능하므로 위와 같이 측정가능한 변수들로 표현해주고
회전자의 쇄교 자속에 대한 식으로 정리한다.


해당 식을 적분한다면 회전좌표계상의 회전자 쇄교 자속을 구할 수 있다. 하지만 d축에는 q축에 대한 변수가 q축에는 d축에 대한 변수가 엮여 있어 이는 연산을 어렵게 만든다.
위 식에서 w는 동기 좌표계(고정자의 회전 좌표계..?)가 회전하는 속도로 2*pi*fe로 구할 수 있다.
그러나 회전자는 w_rm(=0.5*p*w_m)으로 회전하므로 회전자의 회전좌표계는 w_rm의 속도로 회전하고 이 속도 차이가 전압 방정식에 반영된 것이다.
쇄교 자속을 구하기 위해서 고정자의 회전 좌표계와 회전자의 회전 좌표계의 속도가 동일하다고 가정하면 전압 방정식이 단순해진다.

하지만 위 식에서는 회전 좌표계 상의 고정자 전류 성분을 필요로 한다.
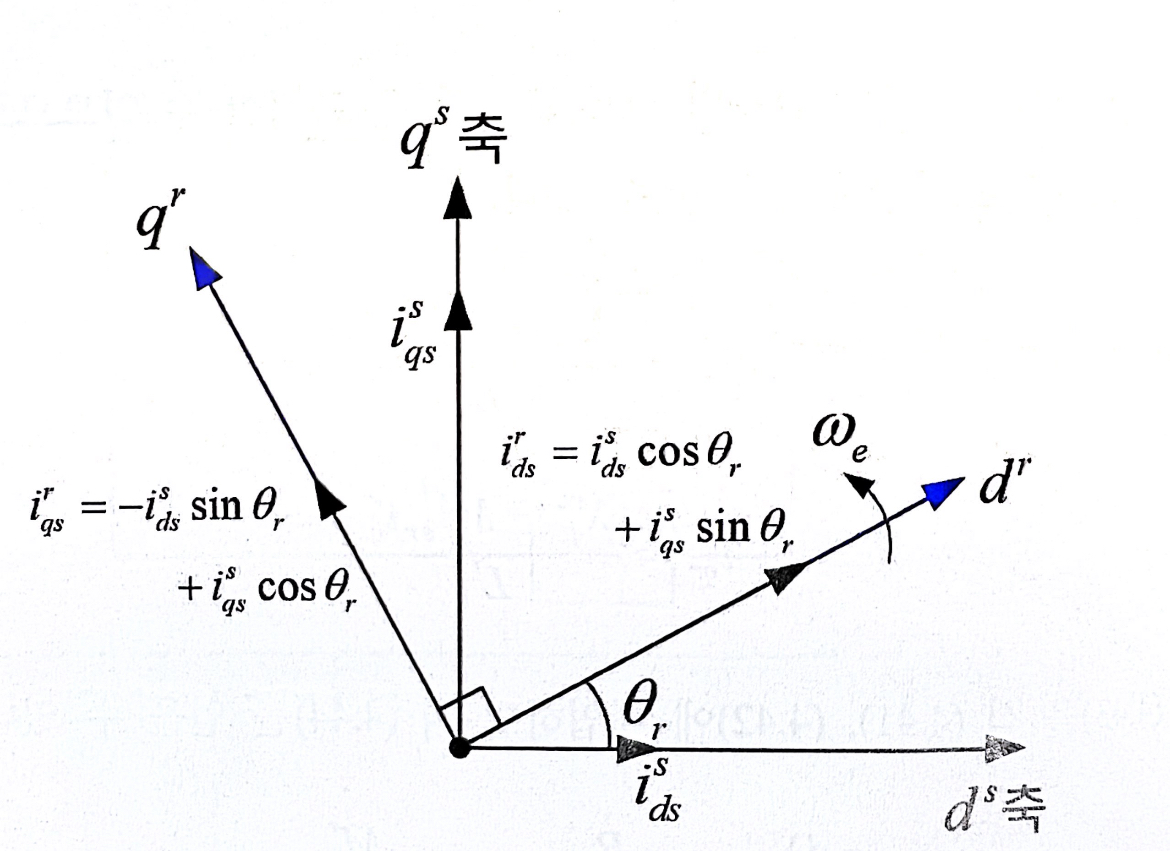
회전 좌표계 성분의 d,q 축 고정자 전류를 정지 좌표계로 정사영 내려 구하는 그림은 위와 같다.
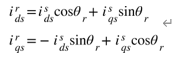
이때 회전각은 회전자 회전속도인 w_rm(=0.5*p*w_m)이나 w_e(=2*pi*f)가 같다고 가정하였으므로 둘 중 하나를 적분해서 구하면 된다.
이것을 종합하여 회전 좌표계 상의 회전자 쇄교 자속을 구할 수 있다.
이를 다시 정사영을 이용해서 정지좌표계 상으로 내리게 된다면 정지 좌표계 상의 회전자 쇄교 자속이 아래와 같이 정리된다.
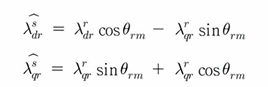
4. 전압 모델과 전류 모델을 모두 사용하는 자속 추정 기법
위에서 구한 두 가지 모델은 각각 유리한 속도 영역이 있다.
전압 모델은 고속에서 유리하고 전류 모델은 저속에서 유리한 특성을 갖고 싶다.
이 특징을 고려하여 두 가지 모델을 결합하여 저속에서는 전류 모델을 고속에서는 전압 모델을 이용하는 혼합 방식이 흔히 사용된다고 한다.
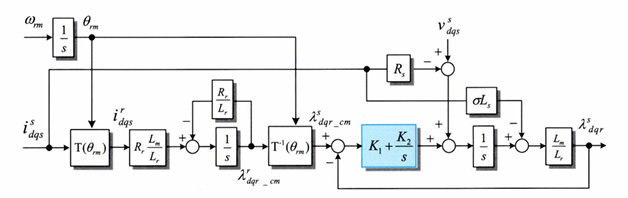
위 블록도는 두 가지 모델을 결합한 것이다.
이때 오른쪽을 보면 PI 제어기와 I제어기를 이용해 필터를 넣은 것을 볼 수 있다.
이 필터를 이용해서 2가지 모델의 부드러운 전이가 가능하도록 하고 있다.
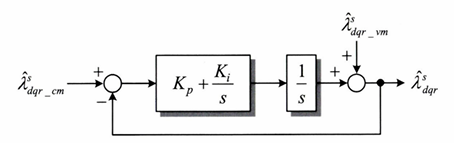
필터 부분만 간략화한 블럭도는 위와 같다.
이때 Lamda_cm은 전류 모델에서 나온 값 Lamda_vm은 전압모델에서 나온 값을 의미한다.
여기서의 전달함수를 구해본다면
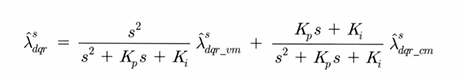
다음과 같이 나오는 것을 볼 수 있다. 이때 전류모델은 2차 LPF, 전압모델은 2차 HPF로 필터링 되는 것을 알게 된다.
이를 고려하여 위 블럭도에서의 적분이득 (K1)과 비례이득 (K2)를 구해보면 다음과 같다.