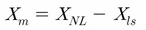이제 유도기가 포함된 MG 세트를 구동하기 앞서, 각 Parameter들을 찾아야 한다.
해당 과정에서는 설승기 교수님의 '전기기기제어론'과 여러 논문을 참고하였다.
우선 동기기부터 진행하려 한다.
1. 고정자 저항 (Rs) 찾기
( 고정자 저항값은 정밀 저항계를 이용해 측정하면 된다.
-> 세부적인 내용은 추후 서술 예정)
부경대 정영석 교수님의 ' 위치센서가 없는 영구자석형 동기전동기의 파라미터 측정' 논문 중

정지 상태의 모터(q축 전원인가 x)에 서로 다른 2개의 d축 전압을 인가하는 방식이 등장한다.
그럴 경우 각각 다른 d축 전류가 흐르고 있을 것이다.
이때 옴의 법칙을 이용하여

해당 수식을 이용하면, 고정자 저항이 나온다고 한다.
여기서 어느정도의 전압을 인가해야하는지는 좀 더 공부해야할 것 같다.
(논문에서는 0.35V로 회전자를 먼저 d축에 align 시켜놓고 0.37V와 0.43V를 인가하여 측정)
(다른 논문에서는 0.05초간 두 번 인가 20V와 10V)
2. 영구자석의 쇄교자속(lam_f) 찾기

동기기의 전압방정식을 보면 위와 같다.
이때 상호성분으로 인해서 q축의 전압에서는 영구자석의 쇄교자속으로 인한 성분이 있다.
만약 우리가 d,q 축의 전류를 모두 0으로 인가한다면,
전류제어기의 출력은 d축은 0 q축은 쇄교자속과 속도가 곱해진 term만 존재한다.
따라서 q축 전압을 속도로 나누어 쇄교자속을 측정할 수 있다.
3. 동기 인덕턴스 찾기
동기 인덕턴스도 마찬가지로 2번의 d축 전압을 인가하여 식별할 수 있다.

전압방정식을 정리하여 인덕턴스에 대한 식으로 표현하면, 다음과 같이 적분 식으로 정리된다.

이때 첫 번째 구간에서의 전압 V1은 다음과 같이 표현된다.

두 번째 구간에서의 전압 V2는 아래와 같다.

두 전압의 차를 구하면, 인덕턴스의 차분항 저항의 차분항 꼴로 식이 정리된다.

우리가 구하고자하는 Ld만 좌변에 놓고 전개하면 아래와 같다.

이때 I2와 I1은 과도상태일 때의 전류값이다.
그리고 Rs에 대한 term은 날리고

위 수식으로 근사해서 인덕턴스를 구할 수 있다,
이때 MG세트의 동기기는 SPMSM으로 d,q축의 인덕턴스가 같으므로 q축을 별도로 다시 측정할 필요는 없다.
(이번에는 0.01초간 두 번인가 10V와 20V)
4. 관성모먼트, 마찰계수 선정
부하토크가 0일 때의 전동기 토크 방정식은 아래와 같다.
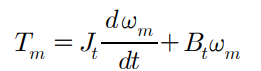
위 두 계수를 찾는 과정에서는 전압이 아닌 토크로 신호를 주입하고
토크가 인가된 시간 t_0~t_1 까지의 구간과 토크가 인가되지 않아 속도가 감소하는 t_1~t_2의 구간으로 나눌 수 있다.
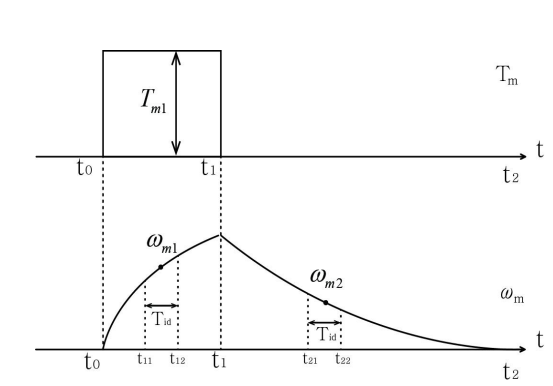
여기서 의문 저기 속도를 측정하는 구간은 어떻게 설정하지,,?
일단 두 구간에 대한 토크 방정식을 쓰면 아래와 같다.
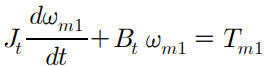
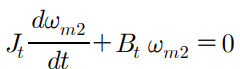
속도의 미분항은 각가속도와 같으므로, 위 식을 각가속도에 대해 다시 쓸 수 있다.
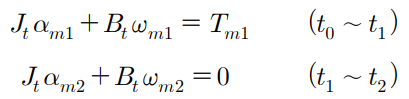
이때 두번 째 구간에 대해 정리한다면, 관성 모먼트를 바로 구할 수 있다.
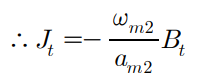
이때 각가속도를 구하는 방법은 뒤에 등장한다.
위 관성 모먼트를 첫 번째 구간에 대입하면 식이 다시 정리된다.
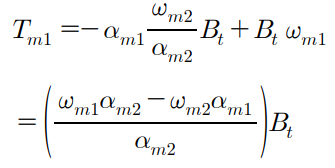
위 식을 다시 정리하면, 마찰계수에 대한 식을 구할 수 있다.
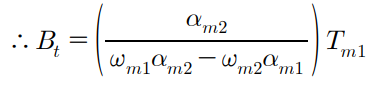
위 식에 대입되는 각속도와 각가속도 값은 아래와 같다.
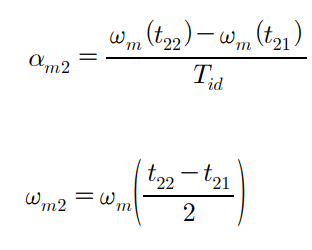
이때 Tid는 100PWM 이상인, 0.00625sec로 선정하였다고 한다.
다음으로는 유도기의 제정수 찾는법에 대해 정리해 보겠다.
1. 고정자 저항 찾기
동기기와 동일하게 q축 전류를 인가하지 않으면, 토크가 발생하지 않아 속도에 대한 역기전력 항이 0이 된다.
따라서 2개의 d축 전압을 인가하고, 2개의 d축 전류를 측정한 후
동기기와 같이 전압의 증가량 / 전류의 증가량의 식을 통해 고정자 저항값을 계산할 수 있다.
2.No load test -> 고정자 인덕턴스
다음으로 무부하 상태에서 유도전동기를 구동하는 No load test가 있다. 해당 시험에서는 기계적으로 아무런 부하도 걸리지 않아야 한다.
현재 연구실의 MG 세트는 두 모터가 커풀링으로 결합된 상태이므로 떼어내기가 어렵다. 따라서 동기기는 아무런 전압도 인가하지 않고, 유도기만 구동하면 되는지 아직 확실치 않다.
우선 무부하 상태는 슬립이 0이라고 볼 수 있다. 이때는
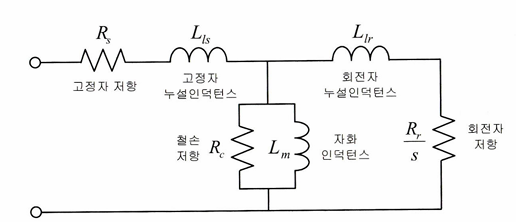
위 회전자 회로에서 회전자 저항과 누설 인덕턴스는 무시할 수 있게 된다.
우선 무부하 조건에서 정격 주파수의 정격 전압을 인가하면 된다.
이때 3상 입력 전력과 선간 전압, 상전류를 측정한다.
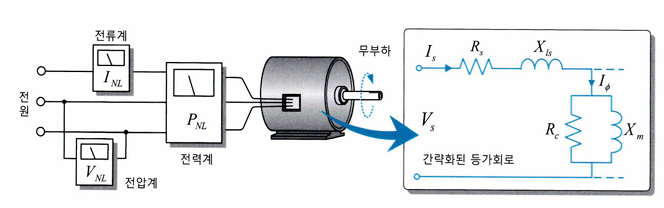
이때 R_c는 동손과 마찰손 등 회전하면서 발생하는 모든 손실을 저항 성분으로 등가한 것이다.
저항을 이용한 전력 구하는 공식을 변형하면, 이 R_c 성분을 계산할 수 있다.
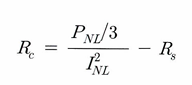
다음으로 선간전압 공식을 이용해 회로의 임피던스 성분과 저항 성분을 측정할 수 있다.
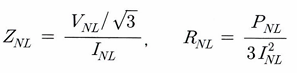
이때, 임피던스의 크기에서 저항 성분의 크기를 뺀다면, 인덕턴스 성분의 합을 알 수 있다.
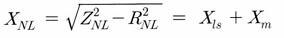
이 값들은 뒤에 이어지는 Blocked Rotor 시험을 통해, 각각의 인덕턴스로 분리할 수 있게 된다.
3. Blocked rotor test -> 회전자 저항, 회전자 인덕턴스
다음으로는 회전자가 움직이지 않도록 구속한 상태에서 진행하는 시험이다.
회전자의 속도가 0이므로 당연히 슬립값은 1과 같다. 이때의 등가회로는 아래와 같다.
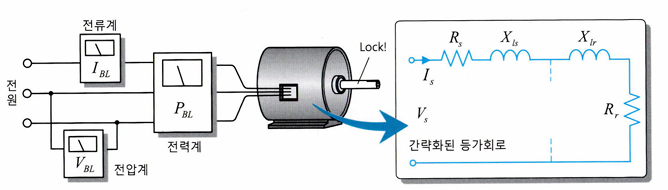
해당 시험에서는 정격 전류가 흐를 수 있게 전압을 인가해야한다.
이때 역시 입력 전력, 선간 전압과 상전류를 측정한다.
이를 조합하여 구한 저항 중 위에서 구한 고정자 저항값을 뺀다면, 회전자 저항값을 구할 수 있다.
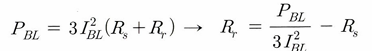
다음으로 다시 임피던스 성분을 구하고 여기서 저항 성분의 크기를 빼면
인덕턴스 성분의 크기를 구할 수 있다.
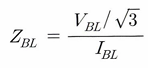
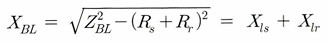
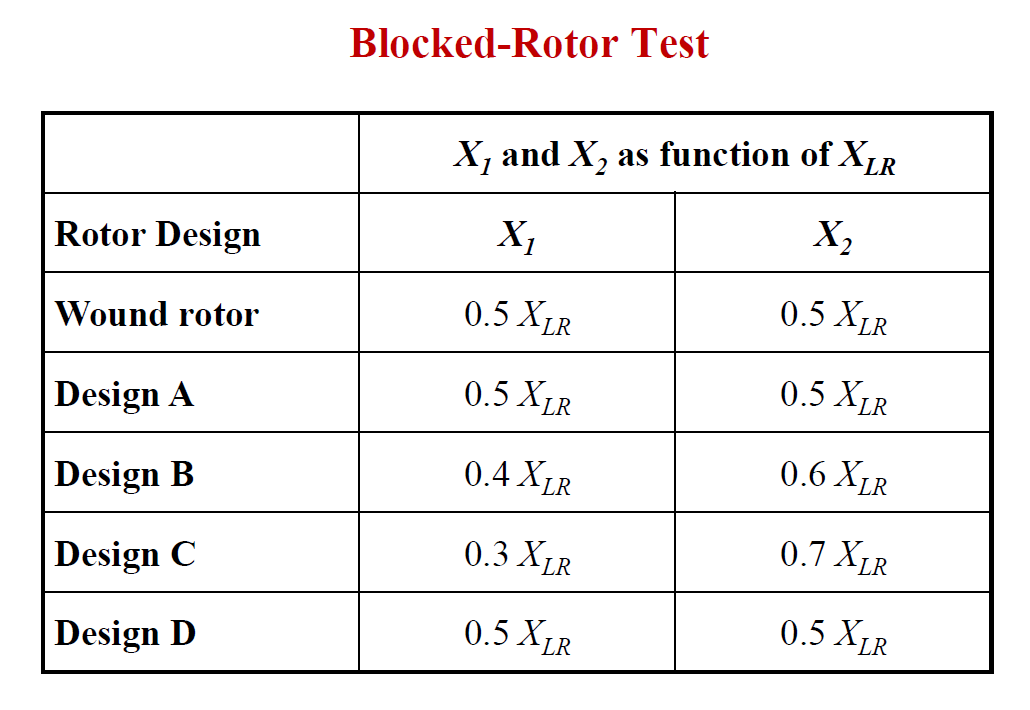
이후 두개의 합성 인덕턴스를 Rotor Design에 따라 위 표를 보고 비율을 맞춰 구할 수 있다,
통상적으로 Xlr과 Xls가 1대 1로 가져가곤 한다.
여기서 Xls 크기를 구했으면 위 무부하 실험에서 구한 합성 인덕턴스를 이용해, Xm도 구할 수 있게 된다.